Assorted CS Topics
Trees
Trees are data structures that are similar to linked lists, but rely on nodes linking to many nodes in a tree-like fashion.
Trees consist of a top node, called the root of the tree, linking to children nodes below it.
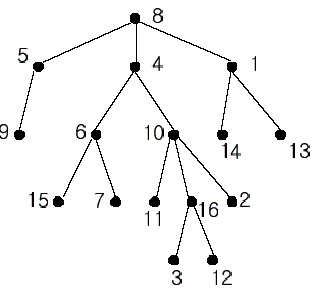
So what's the point? Trees are used in many areas of computer science, including syntax parsers (determines if your parentheses and functions are correct). They're also used in practical applications, such as nested comments and files/directories.
Implementation
Trees are built out of two classes: a Tree class and a TreeNode class.
This is similar to how Linked Lists are built. Linked Lists have a ListNode with
a propery for data and a property next to point to the next node in the list.
A TreeNode has a property to store data, and left and right properties to
store references to branches off the current node off to the left and right.
The Tree class defines one node called the root node which represents the top of the tree.
The root property points to an instance of a TreeNode. The Tree class also houses useful
methods for adding nodes, removing nodes, and printing out the entire tree.
See tree.rb for an actual implementation of TreeNode and Tree classes in Ruby.
Traversing Trees
We can use for loops to iterate over arrays. Arrays have a definite length and all of the indexes are sequential.
We can iterate Linked Lists using while loops. We can set a pointer to the first
node and keep stepping to the next next node until there's no next node left.
Linked Lists are still a linear data structure.
Trees are harder to iterate over. Each Tree Node splits into two more, on it's left and right side. There's no one straight path through a tree. How could we iterate through a tree?
The answer. Is Recursion. For each Tree Node we can print out it's data, then
print out the date for it's left and right side. Traversing a tree looks like this:
def inOrderTraverse(node)
if node != nil
puts node.data
traverse(node.left)
traverse(node.right)
end
end
Notice that there are different orders we can traverse the tree in.
in-order traverse: print node.data, recurse left, recurse right.
pre-order traverse: recurse left, print node.data, recurse right.
post-order traverse: recurse right, print node.data, recurse left.
Practice writing down the in-order, pre-order and post-order traversals for this tree:
4
/ \
1 8
/ \
6 12
Practice Problems
- write a function that counts the total number of nodes in the tree.
- write a function that finds the minimum value in a tree.
Binary Search Trees
The most common tree structure is known as a binary search tree. Each node has at most two children, and they provide a way to order elements. When inserting values, the value goes to the left child if less than the root node, and to the right child if greater than the root node.

Note the mathematical benefits of a binary tree. As we add another "level" to the tree, the number of nodes at that level doubles. Therefore, this can be represented with the equation
2^x = n
where x is the number of levels, and n is the number of nodes. Since it's likely
that we know the number of nodes vs. of the number of levels, we can represent this
equation with logarithms.
x = log(n)
where x is the number of levels, and n is the number of nodes.
Due to the mathematical benefits above, insertion, deletion, and search take an average of O(log(n)) with binary search trees. But there's a worst case scenario.

We just made a bloated linked list! There has to be a better way, and thanks to research, there is.
Balanced Trees
To avoid the worst case scenario of a binary search tree, there are methods to create balanced trees, where we are guaranteed average and worst case runtimes of O(log(n)). A couple methods of doing this include rebalancing the tree based on subtree size and/or categorizing nodes.
Tries
Tries are a special type of tree, usually implemented with strings as the data, where child nodes share a common prefix (as represented by the parent node).

They're usually used for quick lookups, generally autocomplete fields and IP address lookups. Assuming a trie was balanced, what would be the average lookup time for a value?
Sets
A set is a data type that is often implemented with a tree, but can be implemented with various other data structures. Sets are collections of items that are unordered and contain no duplicates. In Ruby and JavaScript, sets are provided as Set. Here are some examples in Ruby:
# must be required
require 'set'
s1 = Set.new([1, 2, 3])
# => #<Set: {1, 2, 3}>
# sets must have unique items, they're also unordered
s2 = Set.new([9, 5, 5, 5, 5])
# => #<Set: {9, 5}>
s3 = Set.new(['taco', 3])
# => #<Set: {"taco", 3}>
# sets have different methods to determine if they share/don't share elements
s1.intersect? s2
# => false
s1.intersect? s3
# => true
s1.disjoint? s2
# => true
s1.disjoint? s3
# => false
# set operations
# union
s1 + s2
# => #<Set: {1, 2, 3, 9, 5}>
# difference
s1 - s3
# => #<Set: {1, 2}>
# intersection
s1 & s3
# => #<Set: {3}>
Graphs
If we remove even more restrictions from trees, we end up with graphs, which are interconnected sets of nodes. Each connection is called an edge.
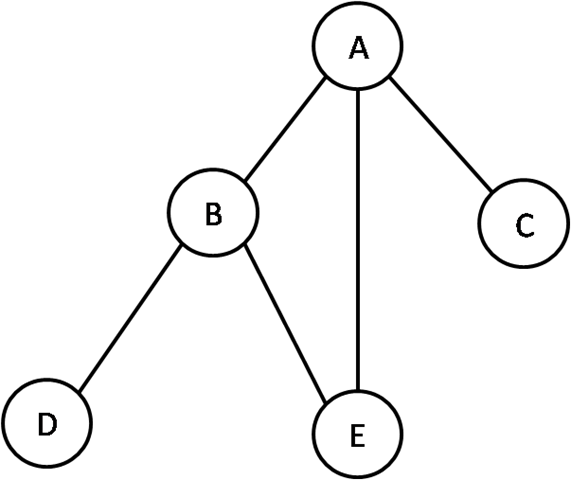

Graphs can be directed (a path that has direction) or undirected. Graphs are essential in applications such as Facebook or Twitter, where showing relationships between users and groups is essential across large applications. Other applications include maze solving and mutual friend finding, which can be implemented via the following graph searches.
Graphs are more than just nodes and edges though. Graph theory categorizes graphs by different properties, such as bipartite, directed, undirected, and more.
Note that we can modify a linked list to be a graph. Instead of having one next pointer, we could have either a list or matrix that shows which edges the graph connects to.
Searching
There's a couple ways to search graphs.
Depth-First Search
Exploring the graph as far as possible, then backtracking.
Breadth-First Search
Exploring the graph close to the starting point, then slowly growing out.