Binary Search

Binary search is an efficient O(log(N)) algorithm for finding elements in a sorted array. It's important that the array is sorted. Binary Search doesn't work on unsorted arrays.

Auto Guess

We previously created a guessing game app that picked a random number and had you guess what it was until you got it correct.

Now we want to make the game guess the number automatically, in as few guesses as possible without teaching.

Binary Search finds items quickly by guessing an array index where an element might be, reading the value at that index, and basing it's next guess on what value it read. If the value at the index was less than the value it's searching for its next guess will be a higher index. It chooses a lower index if the value read was higher than what it is looking for.

Consider How You Use Phonebooks

Imagine flipping through a phone book to find someone's number. A linear O(N) algorithm would start at the beginning of the phone book and read every name on every page until it found the name you're looking for. This is terribly slow!

Instead of reading every single name it's much easier to read one random name and flip far forward or backward depending on how close that name is to the name you're looking for.

This only works because the phone book is sorted by names. Imagine trying to do a reverse look up on a mysterious phone number using a phone book. You'd have to start at the beginning and look at every single entry!

How Fast is Fast?

Imagine we had an array where every array access took 1 second. No matter what index we read it would take a full second for us to get the value. It would take us a minute to read every item in an item with only 60 items in it.

How long is a trillion seconds?

• 1,000 seconds is equal to almost 17 minutes.
• It would take almost 12 days for a million seconds to elapse
• It takes about 31.7 years for a billion seconds to go by.
• A trillion seconds amounts to no less than 31,709.8 years.

It would take practically 31,709 years to search iteratively through an array with one trillion items.

With binary search it would take only 40 guesses to find the correct index. Binary Search reduced the runtime of searching for something in the trillion-length array from 31,709 years to only 40 seconds!

Binary Search is extremely fast.

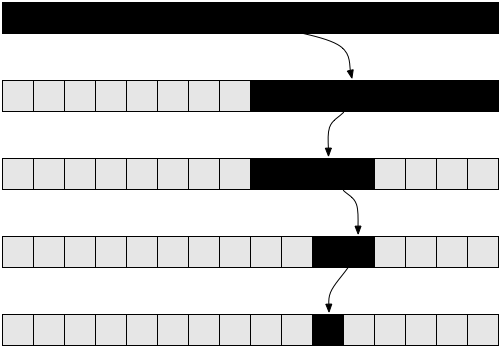
Implement It

Try to implement your own version of binary search. Here's a description of the algorithm to help get you started:

1. set up variables min, max and guess to keep track of the range of indexes you're currently searching through.
2. set guess equal to (min + max / 2) and round it. We'll let you figure out what min and max should be set to at first.
3. read the value of the array at the index of guess
4. if the value read is higher than n then adjust max = guess - 1
5. if the value read is lower than n then adjust min = guess + 1
6. repeat steps 2 through 5 until n is found.
7. return guess as the index of n
8. return -1 if min, max, and guess converge on an index and n is not in the array.

You may assume the given array is sorted. Your code must handle the case when the array is empty.

// search for the index n inside of array
// return the index of n
// return -1 if it doesn't exist
function binarySearch(array, n) {

}

Bonus

Binary Search is able to return useful information even if the element isn't even in the array.

What happens when an element isn't in a array?

var nums = [7, 10, 20, 30, 40, 50, 60]
binarySearch(nums, 15); // returns -1

Here's what happens when Binary Search runs:

guess = 4    // start guessing at 4
nums[4] = 40 // value is higher
guess = 2    // guess lower
nums[2] = 20 // value is higher
guess = 1    // guess lower
nums[1] = 10 // value is lower
guess = 2    // guess higher.  wait! we already guessed this.

It can actually return an index representing where an element should be. Instead of manually returning -1 we can almost return the index of our last guess. The index of our last guess represents where the element would be if it were in the array. Then, we could manually add the item at exactly the correct index and the array would remain sorted.

If we simply return the index of our last guess how would users of our algorithm tell the difference between when the number was found, and when we're trying to tell them the index of where it should go?

Instead of returning the index return the negative index! Now any positive number that comes back from the binary search represents that the element was found there. Any negative number that comes back from the array means that the element wasn't found, but we can do some math on the result and determine where it should be added.

Wait. What's negative zero? Still just zero.

There's one small problem. The zero-index of arrays complicates the idea that we can simply return the negative index of our last guess. If the algorithm returned zero it would be impossible to tell if it meant it found the element at zero, or if it means the element wasn't found and it should be added at element zero.

Instead of returning -guess return -(guess - 1). This shifts zero indexes from zero to negative one. And now our algorithm truly fits these rules:

1. binarySearch(n) >= 0 is the index of the element in the array
2. binarySearch(n) < 0 means the element wasn't found.

If binary search returns a negative number we can add 1 to it and negate it to determine where a non-found element should be inserted.

var index = binarySearch(n);
var insertIndex = undefined;

if (index < 0) {
  insertIndex = -(index + 1);
}