Computer Science Intro

Objectives:

After this students will be able to:

find a value in an array in a slow and fast way
understand the graph of the time complexity of a function
use the concept of algorithmic complexity to differentiate a fast algorithm from a slow one

Introduction 5 mins

what is computer science?
- study of how to do "computation"
- computing things in a theoretical, hardware independent, mathematically way
- reducing these ideas to provable formulas / proofs
- understanding what we can compute, how long it will take, what kind of resources it will take up (RAM, disk space, Gzh processing, etc)
why do we want to learn this stuff?
- one layer above / more abstract than programming
- abstractions of these problems permeate literally every piece of software you interact with:
- https://medium.com/@_marcos_otero/the-real-10-algorithms-that-dominate-our-world-e95fa9f16c04
- tells you how to do things at "internet scale", i.e. very large systems ( things you do more than 10 times )
- shows understanding during job interviews

What are algorithms? 5 mins [10mins in]

you've already been writing algorithms
making a PB&J sandwich is an algorithm
studying algorithms means studying how a given algorithm behaves as the inputs grow

Data Structures

Are the containers we put data into, and run the algorithms on.

Isn't one way to do things the same as all the others? ( how many ways can there be to make a pb&j sandwich )

lets consider a simple alogrithm that finds a value in an array:

Linear Search (pairing exercise) 5mins [15 mins in]

split the students into pairs
for a sorted array we will find some arbitrary value inside this array

given this code:

var stuff = [10,34,56,67,93,120,137,168,259,280,311,342,413,514];
var random_value = stuff[ Math.ceil( Math.random() * 14 ) ];

write a for loop that looks at each index of the array to see if it matches the random value
if it does match the random value display an alert box with the index of the array and the value
linear search is just a fancy way of saying a for loop with a conditional

Solution:

for( var i=0; i<stuff.length; i++ ){

  if( stuff[i] === random_value ){

    alert( i + " : " + random_value );
  }
}

Linear Search: Discussion 10 mins [25 mins in]

pseudo code:

For each item in the list:
   if that item has the desired value,
       stop the search and return the item's location.
Return Λ.

how long does this algorithm take? (what is it's running time)
it will take between 1 and 14 tries depending on the randomly generated thign we are searching for
how can we think about a generalizes way to describe how long this algorithm takes?
- also: let's think about what "how long this takes" means:
- how do we describe this in a way that only applies to the algorithm itself and not to the computer it runs on or the language you're using or whether or not someone trips over the power cord as you are running this program?
- we can speak in terms of instructions to the computer, each thing we ask the computer to do can be counted as taking a bit longer
- we asked the computer to do stuff.length things, plus run an alert
- in math terms we asked the computer to do a maximum of 14 things, or n things
- this is the "complexity" or "runtime" of one piece of code, independent of it's hardware implementation

Changing inputs: graphs and how to define efficiency [10 mins] [35 mins in]

consider if we made these changes in the way that stuff is created:

var stuff = [];

var max_size = 1000000000;

var size = Math.ceil( Math.random() * max_size );

for( var j=0; j<size; j++ ){

  stuff.push( j+1 );
}

var random_value = Math.ceil( Math.random() * size );

have a student explain to the class what this code does
If we use the same for loop (search algorithm) to find random_value how can we describe how long it will take?
It will take between 1 and (size of array) times to find, between 1 and n times to find.

Big-O: How we describe algorithm efficiency [10 mins] [45 mins in]]

In CS we generally describe the efficiency of something as it's longest possible run time
equivalent to max_size in the example above
We want to understand how this algorithm behaves as we increase or decrease max_size
This is "Big-O": The graph of the run time of an algorithm's worst case performance as the input size grows
on the board teacher draws a graph of the efficiency of the algorithm as max_size grows larger
- what is the number of things that happen
- calculate the actual number of times the algorithm runs for the first 4 or 5 input sizes
- extend the line of the graph or draw another graph that extrapolates those 4 or 5 numbers
we want a picture of the behavior of this function as max_size get bigger and bigger to be as generalized as possible
- thanks to the properties of polynomial functions / graphs, when we said above that our algorithm takes f(n)+1 or O(n)+1 time to run, we can say that it is basically equivalent to taking n time to run - (the graph of that function doesn't differ too greatly from a function with other similar terms)
- Big-O in this sense is a classifying tool used to generalize the complexity of an algorithm-
- We can use it to determine the complexity difference between something O(n²) to O(2ⁿ) - a huge diference!
- ( if n is 10, 10^2- n squared- is 100, 2^10th is 1024 )
- "operations" (runtime) as we've defined them basically amount to loops, number of loops your program needs to run

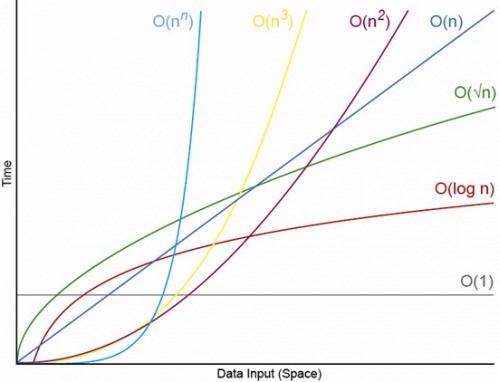
Isn't it all the same anyways? (15 mins) [1 hr in]

lets look at the most efficeint way possible to fins this same value:
binary search

we started with a for loop: (linear search)

for( var i=0; i<stuff.length; i++ ){

if( stuff[i] === random_value ){

  alert( i + " : " + random_value );
}
}

let's look at something more efficient:
teacher explains each step of the algorithm:
- use the provided binarySearch.html file
- divide array in half
- is that the number?
- if not, is the number more or less than current
- repeat with new subdivided thing
- like a number guessing game:
  - I'm thinking of a number between 1 and 1000
  - linear search- ask for each number starting from 0
  - binary search:
    - is it 500? is it lower or higher than 500? etc., etc.
every step discards large chucks of possible things to look at
very efficient

pseudo code:

int binary_search(int A[], int key, int imin, int imax)
{
// continue searching while [imin,imax] is not empty
while (imin <= imax)
  {
    // calculate the midpoint for roughly equal partition
    int imid = midpoint(imin, imax);
    if (A[imid] == key)
      // key found at index imid
      return imid;
    // determine which subarray to search
    else if (A[imid] < key)
      // change min index to search upper subarray
      imin = imid + 1;
    else        
      // change max index to search lower subarray
      imax = imid - 1;
  }
// key was not found
return KEY_NOT_FOUND;
}

It's not all the same (5 mins) Teacher Talks [1 hr 5 mins in]

talk about what kinds of differences algorithm choice can make
how and why this algo is more efficient
- runs in O(logn)
- teacher refers back to comparison graphs
caveats and limitations
- array must be sorted
- what if the array is only ever 2 elements? is it still more efficient?
"operations" (runtime) as we've defined them basically amount to loops, number of loops your program needs to run

Actually how much longer? Students Do (5 mins) [1 hr 10 mins in]

what if max_size is 1 million, linear vs binary search?
ask students to figure out how much longer it will take
what is the worst case for each search algorithm

How fast is your code? (pairing exercise) 20 minutes

One person in your pair will find an algorithm their your code. Figure out what the big-O of it is.

Space complexity Teacher Talks (5 mins) [1hr 15 mins in]

we won't talk about space complexity in detail
how much memory something takes up- how many "storage / comparison" variables do we use when we run an algorithm
we can denote this with the same Bio-O notation

How to Choose an algorithm for a given situation.

what are the starting conditions for the algorithm to run?
- does the data need to be sorted? (i.e. binary search)
- do I need to know the key I am looking for? (i.e. hash table)
do you know ahead of time the size of the inputs?
- will it always be very large or very small?
- will each element of the inpout be very large? (i.e. 4k video frames vs. 480p video frames)
is the actual speed of the alogrithm a concern?
- is it a cost issue? (total cost to process something)
- is it a user experience issue? (UI freezes while processing)
meta conditions
- do you even need to solve this problem
- what are some workarounds
- cost / benefit
  - is the final computation / dollar / development cost worth it
  - code compliexity vs. maintainability / development time

Conclusion

what is the implementation of search algorithms good for?
not much
you will probably never implement a search algorithm
wanted to show how a simple algorithm type can have fast and slow implmentations
easy way to talk about Big-O

Computer Science